Determine network properties for objects of class
microNet.
Usage
netAnalyze(net,
# Centrality related:
centrLCC = TRUE,
weightDeg = FALSE,
normDeg = TRUE,
normBetw = TRUE,
normClose = TRUE,
normEigen = deprecated(),
# Cluster related:
clustMethod = NULL,
clustPar = NULL,
clustPar2 = NULL,
weightClustCoef = TRUE,
# Hub related:
hubPar = "eigenvector",
hubQuant = 0.95,
lnormFit = FALSE,
# Graphlet related:
graphlet = TRUE,
orbits = c(0, 2, 5, 7, 8, 10, 11, 6, 9, 4, 1),
gcmHeat = TRUE,
gcmHeatLCC = TRUE,
# Further arguments:
avDissIgnoreInf = FALSE,
sPathAlgo = "dijkstra",
sPathNorm = TRUE,
normNatConnect = TRUE,
connectivity = TRUE,
verbose = 1
)Arguments
- net
object of class
microNet(returned bynetConstruct).- centrLCC
logical indicating whether to compute centralities only for the largest connected component (LCC). If
TRUE(default), centrality values of disconnected components are zero.- weightDeg
logical. If
TRUE, the weighted degree is used (seestrength). Default isFALSE. Is automatically set toTRUEfor a fully connected (dense) network.- normDeg, normBetw, normClose, normEigen
logical. If
TRUE(default for all measures), a normalized version of the respective centrality values is returned.- clustMethod
character indicating the clustering algorithm. Possible values are
"hierarchical"for a hierarchical algorithm based on dissimilarity values, or the clustering methods provided by the igraph package (seecommunitiesfor possible methods). Defaults to"cluster_fast_greedy"for association-based networks and to"hierarchical"for sample similarity networks.- clustPar
list with parameters passed to the clustering functions. If hierarchical clustering is used, the parameters are passed to
hclustandcutree(default islist(method = "average", k = 3).- clustPar2
same as
clustParbut for the second network. IfNULLandnetcontains two networks,clustParis used for the second network as well.- weightClustCoef
logical indicating whether (global) clustering coefficient should be weighted (
TRUE, default) or unweighted (FALSE).- hubPar
character vector with one or more elements (centrality measures) used for identifying hub nodes. Possible values are
degree,betweenness,closeness, andeigenvector. If multiple measures are given, hubs are nodes with highest centrality for all selected measures. See details.- hubQuant
quantile used for determining hub nodes. Defaults to 0.95.
- lnormFit
hubs are nodes with a centrality value above the 95% quantile of the fitted log-normal distribution (if
lnormFit = TRUE) or of the empirical distribution of centrality values (lnormFit = FALSE; default).- graphlet
logical. If
TRUE(default), graphlet-based network properties are computed: orbit counts as defined byorbitsand the corresponding Graphlet Correlation Matrix (gcm).- orbits
numeric vector with integers from 0 to 14 defining the orbits used for calculating the GCM. Minimum length is 2. Defaults to c(0, 1, 2, 4, 5, 6, 7, 8, 9, 10, 11), thus excluding redundant orbits such as the orbit o3.
- gcmHeat
logical indicating if a heatmap of the GCM(s) should be plotted. Default is
TRUE.- gcmHeatLCC
logical. The GCM heatmap is plotted for the LCC if
TRUE(default) and for the whole network ifFALSE.- avDissIgnoreInf
logical indicating whether to ignore infinities when calculating the average dissimilarity. If
FALSE(default), infinity values are set to 1.- sPathAlgo
character indicating the algorithm used for computing the shortest paths between all node pairs.
distances(igraph) is used for shortest path calculation. Possible values are: "unweighted", "dijkstra" (default), "bellman-ford", "johnson", or "automatic" (the fastest suitable algorithm is used). The shortest paths are needed for the average (shortest) path length and closeness centrality.- sPathNorm
logical. If
TRUE(default), shortest paths are normalized by average dissimilarity (only connected nodes are considered), i.e., a path is interpreted as steps with average dissimilarity. IfFALSE, the shortest path is the minimum sum of dissimilarities between two nodes.- normNatConnect
logical. If
TRUE(default), the normalized natural connectivity is returned.- connectivity
logical. If
TRUE(default), edge and vertex connectivity are calculated. Might be disabled to reduce execution time.- verbose
integer indicating the level of verbosity. Possible values:
"0": no messages,"1": only important messages,"2"(default): all progress messages are shown. Can also be logical.
Value
An object of class microNetProps containing the following
elements:
lccNames1, lccNames2 | Names of nodes in the largest connected component(s). |
compSize1, compSize2 | Matrix/matrices with component sizes (1st row: sizes; 2nd row: number of components with the respective size) |
clustering | Determined clusters in the whole network (and corresponding trees if hierarchical clustering is used) |
clusteringLCC | Clusters (and optional trees) of the largest connected component. |
centralities | Centrality values |
hubs | Names of hub nodes |
globalProps | Global network properties of the whole network. |
globalPropsLCC | Global network properties of the largest component. |
graphlet | Graphlet-based properties (orbit counts and GCM). |
graphletLCC | Graphlet-based properties of the largest connected component. |
paramsProperties | Given parameters used for network analysis |
paramsNetConstruct | Parameters used for network construction
(inherited from netConstruct). |
input | Input inherited from netConstruct. |
isempty | Indicates whether network(s) is/are empty. |
Details
Definitions:
- (Connected) Component
Subnetwork where any two nodes are connected by a path.
- Number of components
Number of connected components. Since a single node is connected to itself by the trivial path, each single node is a component.
- Largest connected component (LCC)
The connected component with highest number of nodes.
- Shortest paths
Computed using
distances. The algorithm is defined viasPathAlgo. Normalized shortest paths (ifsPathNormisTRUE) are calculated by dividing the shortest paths by the average dissimilarity (see below).
Global network properties:
- Relative LCC size
= (# nodes in the LCC) / (# nodes in the complete network)
- Clustering Coefficient
The weighted (global) clustering coefficient is the arithmetic mean of the local clustering coefficient defined by Barrat et al. (computed by
transitivitywith type = "barrat"), where NAs are ignored.
The unweighted (global) clustering coefficient is computed usingtransitivitywith type = "global".- Modularity
The modularity score for the determined clustering is computed using
modularity.igraph.- Positive edge percentage
Percentage of edges with positive estimated association of the total number of edges.
- Edge density
Computed using
edge_density.- Natural connectivity
Computed using
natural.connectivity. The "norm" parameter is defined bynormNatConnect.- Vertex / Edge connectivity
Computed using
vertex_connectivityandedge_connectivity. Both equal zero for a disconnected network.- Average dissimilarity
Computed as the mean of dissimilarity values (lower triangle of
dissMat). ByavDissIgnoreInfis specified whether to ignore infinite dissimilarities. The average dissimilarity of an empty network is 1.- Average path length
Computed as the mean of shortest paths (normalized or unnormalized). The av. path length of an empty network is 1.
Clustering algorithms:
- Hierarchical clustering
Based on dissimilarity values. Computed using
hclustandcutree.- cluster_optimal
Modularity optimization. See
cluster_optimal.- cluster_fast_greedy
Fast greedy modularity optimization. See
cluster_fast_greedy.- cluster_louvain
Multilevel optimization of modularity. See
cluster_louvain.- cluster_edge_betweenness
Based on edge betweenness. Dissimilarity values are used. See
cluster_edge_betweenness.- cluster_leading_eigen
Based on leading eigenvector of the community matrix. See
cluster_leading_eigen.- cluster_spinglass
Find communities via spin-glass model and simulated annealing. See
cluster_spinglass.- cluster_walktrap
Find communities via short random walks. See
cluster_walktrap.
Hubs:
Hubs are nodes with highest centrality values for one or more
centrality measures. The "highest values" regarding a centrality
measure are defined as values lying above a certain quantile (defined by
hubQuant) either of the empirical distribution of the centralities
(if lnormFit = FALSE) or of the fitted log-normal distribution
(if lnormFit = TRUE; fitdistr is used for
fitting). The quantile is set using hubQuant.
If clustPar contains multiple measures, the centrality values of a
hub node must be above the given quantile for all measures at the same time.
Centrality measures:
Via centrLCC is decided whether centralities should be calculated
for the whole network or only for the largest connected component. In the
latter case (centrLCC = FALSE), nodes outside the LCC have a
centrality value of zero.
- Degree
The unweighted degree (normalized and unnormalized) is computed using
degree, and the weighted degree usingstrength.- Betweenness centrality
The unnormalized and normalized betweenness centrality is computed using
betweenness.- Closeness centrality
Unnormalized: closeness = sum(1/shortest paths)
Normalized: closeness_unnorm = closeness / (# nodes – 1)- Eigenvector centrality
If
centrLCC == FALSEand the network consists of more than one components: The eigenvector centrality (EVC) is computed for each component separately (usingeigen_centrality) and scaled according to component size to overcome the fact that nodes in smaller components have a higher EVC. IfnormEigen == TRUE, the EVC values are divided by the maximum EVC value. EVC of single nodes is zero.
Otherwise, the EVC is computed for the LCC usingeigen_centrality(scale argument is set according tonormEigen).
Graphlet-based properties:
- Orbit counts
Count of node orbits in graphlets with 2 to 4 nodes. See Hocevar and Demsar (2016) for details. The
count4function fromorcapackage is used for orbit counting.- Graphlet Correlation Matrix (GCM)
Matrix with Spearman's correlations between the network's (non-redundant) node orbits (Yaveroglu et al., 2014).
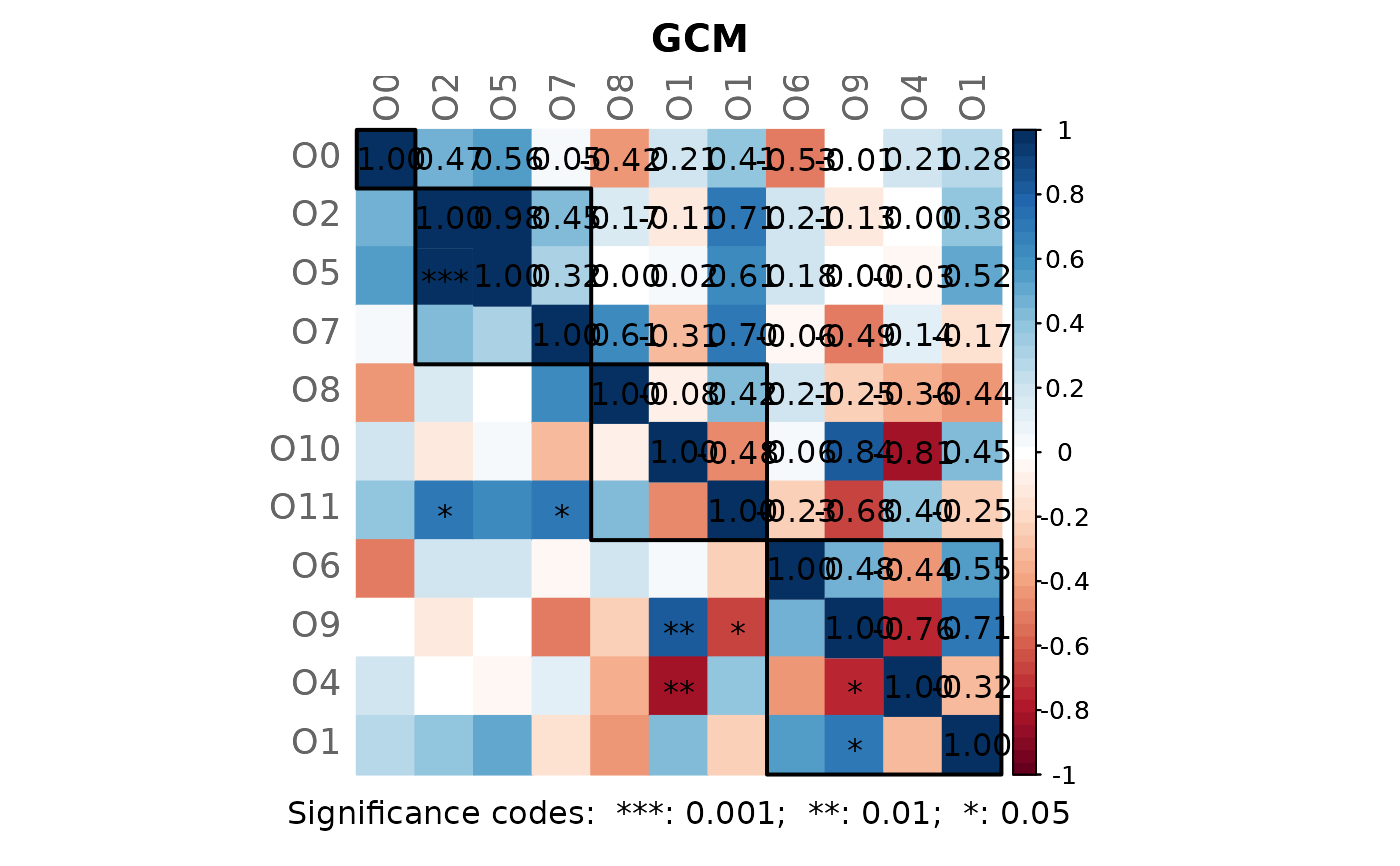
By default, only the 11 non-redundant orbits are used. These are grouped according to their role: orbit 0 represents the degree, orbits (2, 5, 7) represent nodes within a chain, orbits (8, 10, 11) represent nodes in a cycle, and orbits (6, 9, 4, 1) represent a terminal node.
References
Hocevar T, Demsar J (2016). “Computation of graphlet orbits for nodes and
edges in sparse graphs.” Journal of Statistical Software,
71, 1–24.
Yaveroglu ON, Malod-Dognin N, Davis D, Levnajic Z, Janjic V, Karapandza R,
Stojmirovic A, Przulj N (2014). “Revealing the hidden language of complex
networks.” Scientific reports, 4(1), 1–9.
See also
netConstruct for network construction,
netCompare for network comparison,
diffnet for constructing differential networks,
plot.microNetProps for the plot method, and
summary.microNetProps for the summary method.
Examples
knitr::opts_chunk$set(fig.width = 8, fig.height = 8)
# Load data sets from American Gut Project (from SpiecEasi package)
data("amgut1.filt")
# Network construction
amgut_net1 <- netConstruct(amgut1.filt, measure = "pearson",
filtTax = "highestVar",
filtTaxPar = list(highestVar = 50),
zeroMethod = "pseudoZO", normMethod = "clr",
sparsMethod = "threshold", thresh = 0.4)
#> Checking input arguments ...
#> Done.
#> Data filtering ...
#> 77 taxa removed.
#> 50 taxa and 289 samples remaining.
#>
#> Zero treatment:
#> Zero counts replaced by 1
#>
#> Normalization:
#> Execute clr(){SpiecEasi} ...
#> Done.
#>
#> Calculate 'pearson' associations ...
#> Done.
#>
#> Sparsify associations via 'threshold' ...
#> Done.
# Network analysis
# Using eigenvector centrality as hub score
amgut_props1 <- netAnalyze(amgut_net1, clustMethod = "cluster_fast_greedy",
hubPar = "eigenvector")
 summary(amgut_props1, showCentr = "eigenvector", numbNodes = 15L, digits = 3L)
#>
#> Component sizes
#> ```````````````
#> size: 12 6 2 1
#> #: 1 1 1 30
#> ______________________________
#> Global network properties
#> `````````````````````````
#> Largest connected component (LCC):
#>
#> Relative LCC size 0.240
#> Clustering coefficient 0.733
#> Modularity 0.338
#> Positive edge percentage 86.364
#> Edge density 0.333
#> Natural connectivity 0.190
#> Vertex connectivity 1.000
#> Edge connectivity 1.000
#> Average dissimilarity* 0.820
#> Average path length** 1.526
#>
#> Whole network:
#>
#> Number of components 33.000
#> Clustering coefficient 0.523
#> Modularity 0.512
#> Positive edge percentage 89.286
#> Edge density 0.023
#> Natural connectivity 0.028
#> -----
#> *: Dissimilarity = 1 - edge weight
#> **: Path length = Units with average dissimilarity
#>
#> ______________________________
#> Clusters
#> - In the whole network
#> - Algorithm: cluster_fast_greedy
#> ````````````````````````````````
#>
#> name: 0 1 2 3 4 5
#> #: 30 6 4 2 5 3
#>
#> ______________________________
#> Hubs
#> - In alphabetical/numerical order
#> - Based on empirical quantiles of centralities
#> ```````````````````````````````````````````````
#> 119010
#> 71543
#> 9715
#>
#> ______________________________
#> Centrality measures
#> - In decreasing order
#> - Centrality of disconnected components is zero
#> ````````````````````````````````````````````````
#> Eigenvector centrality (normalized):
#>
#> 9715 1.000
#> 119010 0.733
#> 71543 0.723
#> 9753 0.670
#> 307981 0.670
#> 301645 0.670
#> 305760 0.669
#> 512309 0.607
#> 188236 0.131
#> 364563 0.026
#> 326792 0.023
#> 311477 0.005
#> 73352 0.000
#> 331820 0.000
#> 248140 0.000
# Using degree, betweenness and closeness centrality as hub scores
amgut_props2 <- netAnalyze(amgut_net1, clustMethod = "cluster_fast_greedy",
hubPar = c("degree", "betweenness", "closeness"))
summary(amgut_props2, showCentr = "all", numbNodes = 5L, digits = 5L)
#>
#> Component sizes
#> ```````````````
#> size: 12 6 2 1
#> #: 1 1 1 30
#> ______________________________
#> Global network properties
#> `````````````````````````
#> Largest connected component (LCC):
#>
#> Relative LCC size 0.24000
#> Clustering coefficient 0.73277
#> Modularity 0.33781
#> Positive edge percentage 86.36364
#> Edge density 0.33333
#> Natural connectivity 0.19028
#> Vertex connectivity 1.00000
#> Edge connectivity 1.00000
#> Average dissimilarity* 0.82023
#> Average path length** 1.52564
#>
#> Whole network:
#>
#> Number of components 33.00000
#> Clustering coefficient 0.52341
#> Modularity 0.51212
#> Positive edge percentage 89.28571
#> Edge density 0.02286
#> Natural connectivity 0.02791
#> -----
#> *: Dissimilarity = 1 - edge weight
#> **: Path length = Units with average dissimilarity
#>
#> ______________________________
#> Clusters
#> - In the whole network
#> - Algorithm: cluster_fast_greedy
#> ````````````````````````````````
#>
#> name: 0 1 2 3 4 5
#> #: 30 6 4 2 5 3
#>
#> ______________________________
#> Hubs
#> - In alphabetical/numerical order
#> - Based on empirical quantiles of centralities
#> ```````````````````````````````````````````````
#> No hubs detected.
#> ______________________________
#> Centrality measures
#> - In decreasing order
#> - Centrality of disconnected components is zero
#> ````````````````````````````````````````````````
#> Degree (normalized):
#>
#> 9715 0.14286
#> 188236 0.10204
#> 307981 0.08163
#> 71543 0.08163
#> 512309 0.08163
#>
#> Betweenness centrality (normalized):
#>
#> 9715 0.50909
#> 188236 0.47273
#> 307981 0.36364
#> 364563 0.18182
#> 73352 0.00000
#>
#> Closeness centrality (normalized):
#>
#> 305760 2.17422
#> 301645 2.13487
#> 307981 2.12892
#> 119010 1.36913
#> 71543 1.33707
#>
#> Eigenvector centrality (normalized):
#>
#> 9715 1.00000
#> 119010 0.73317
#> 71543 0.72255
#> 9753 0.67031
#> 307981 0.67026
# Calculate centralities only for the largest connected component
amgut_props3 <- netAnalyze(amgut_net1, centrLCC = TRUE,
clustMethod = "cluster_fast_greedy",
hubPar = "eigenvector")
summary(amgut_props3, showCentr = "none", clusterLCC = TRUE)
#>
#> Component sizes
#> ```````````````
#> size: 12 6 2 1
#> #: 1 1 1 30
#> ______________________________
#> Global network properties
#> `````````````````````````
#> Largest connected component (LCC):
#>
#> Relative LCC size 0.24000
#> Clustering coefficient 0.73277
#> Modularity 0.33781
#> Positive edge percentage 86.36364
#> Edge density 0.33333
#> Natural connectivity 0.19028
#> Vertex connectivity 1.00000
#> Edge connectivity 1.00000
#> Average dissimilarity* 0.82023
#> Average path length** 1.52564
#>
#> Whole network:
#>
#> Number of components 33.00000
#> Clustering coefficient 0.52341
#> Modularity 0.51212
#> Positive edge percentage 89.28571
#> Edge density 0.02286
#> Natural connectivity 0.02791
#> -----
#> *: Dissimilarity = 1 - edge weight
#> **: Path length = Units with average dissimilarity
#>
#> ______________________________
#> Clusters
#> - In the LCC
#> - Algorithm: cluster_fast_greedy
#> ````````````````````````````````
#>
#> name: 1 2 3
#> #: 4 5 3
#>
#> ______________________________
#> Hubs
#> - In alphabetical/numerical order
#> - Based on empirical quantiles of centralities
#> ```````````````````````````````````````````````
#> 119010
#> 71543
#> 9715
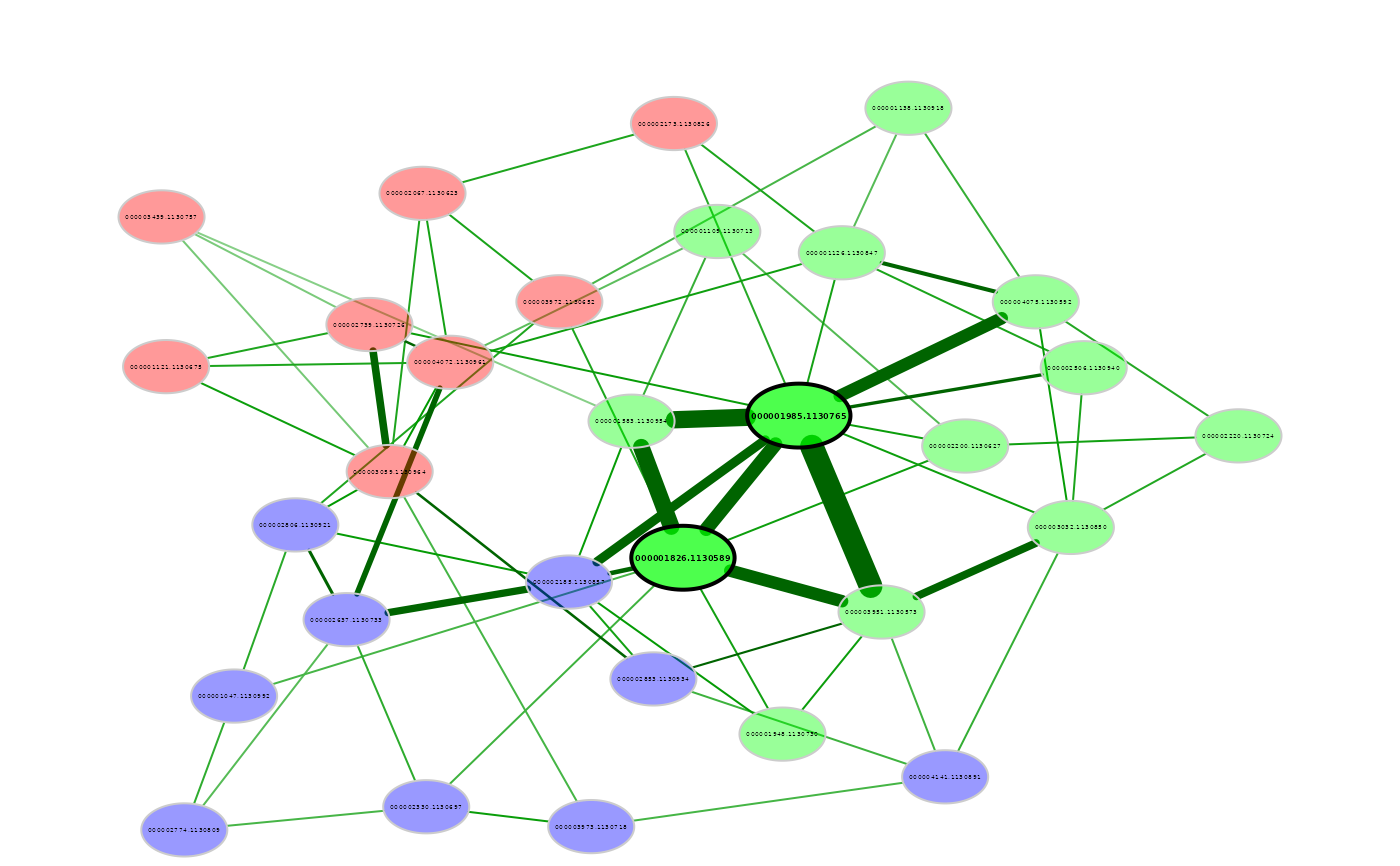
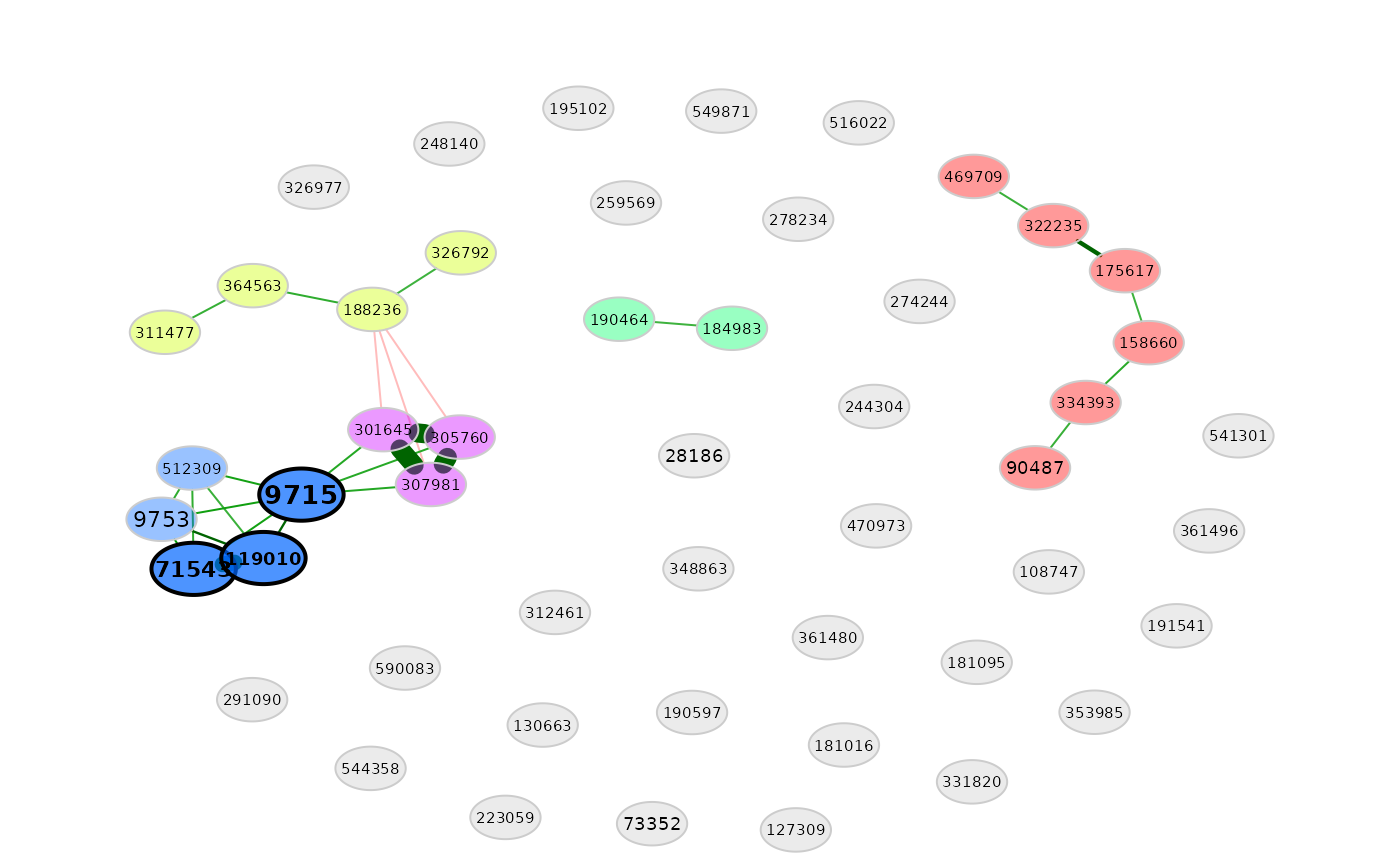
# Network plot
plot(amgut_props1)
summary(amgut_props1, showCentr = "eigenvector", numbNodes = 15L, digits = 3L)
#>
#> Component sizes
#> ```````````````
#> size: 12 6 2 1
#> #: 1 1 1 30
#> ______________________________
#> Global network properties
#> `````````````````````````
#> Largest connected component (LCC):
#>
#> Relative LCC size 0.240
#> Clustering coefficient 0.733
#> Modularity 0.338
#> Positive edge percentage 86.364
#> Edge density 0.333
#> Natural connectivity 0.190
#> Vertex connectivity 1.000
#> Edge connectivity 1.000
#> Average dissimilarity* 0.820
#> Average path length** 1.526
#>
#> Whole network:
#>
#> Number of components 33.000
#> Clustering coefficient 0.523
#> Modularity 0.512
#> Positive edge percentage 89.286
#> Edge density 0.023
#> Natural connectivity 0.028
#> -----
#> *: Dissimilarity = 1 - edge weight
#> **: Path length = Units with average dissimilarity
#>
#> ______________________________
#> Clusters
#> - In the whole network
#> - Algorithm: cluster_fast_greedy
#> ````````````````````````````````
#>
#> name: 0 1 2 3 4 5
#> #: 30 6 4 2 5 3
#>
#> ______________________________
#> Hubs
#> - In alphabetical/numerical order
#> - Based on empirical quantiles of centralities
#> ```````````````````````````````````````````````
#> 119010
#> 71543
#> 9715
#>
#> ______________________________
#> Centrality measures
#> - In decreasing order
#> - Centrality of disconnected components is zero
#> ````````````````````````````````````````````````
#> Eigenvector centrality (normalized):
#>
#> 9715 1.000
#> 119010 0.733
#> 71543 0.723
#> 9753 0.670
#> 307981 0.670
#> 301645 0.670
#> 305760 0.669
#> 512309 0.607
#> 188236 0.131
#> 364563 0.026
#> 326792 0.023
#> 311477 0.005
#> 73352 0.000
#> 331820 0.000
#> 248140 0.000
# Using degree, betweenness and closeness centrality as hub scores
amgut_props2 <- netAnalyze(amgut_net1, clustMethod = "cluster_fast_greedy",
hubPar = c("degree", "betweenness", "closeness"))
summary(amgut_props2, showCentr = "all", numbNodes = 5L, digits = 5L)
#>
#> Component sizes
#> ```````````````
#> size: 12 6 2 1
#> #: 1 1 1 30
#> ______________________________
#> Global network properties
#> `````````````````````````
#> Largest connected component (LCC):
#>
#> Relative LCC size 0.24000
#> Clustering coefficient 0.73277
#> Modularity 0.33781
#> Positive edge percentage 86.36364
#> Edge density 0.33333
#> Natural connectivity 0.19028
#> Vertex connectivity 1.00000
#> Edge connectivity 1.00000
#> Average dissimilarity* 0.82023
#> Average path length** 1.52564
#>
#> Whole network:
#>
#> Number of components 33.00000
#> Clustering coefficient 0.52341
#> Modularity 0.51212
#> Positive edge percentage 89.28571
#> Edge density 0.02286
#> Natural connectivity 0.02791
#> -----
#> *: Dissimilarity = 1 - edge weight
#> **: Path length = Units with average dissimilarity
#>
#> ______________________________
#> Clusters
#> - In the whole network
#> - Algorithm: cluster_fast_greedy
#> ````````````````````````````````
#>
#> name: 0 1 2 3 4 5
#> #: 30 6 4 2 5 3
#>
#> ______________________________
#> Hubs
#> - In alphabetical/numerical order
#> - Based on empirical quantiles of centralities
#> ```````````````````````````````````````````````
#> No hubs detected.
#> ______________________________
#> Centrality measures
#> - In decreasing order
#> - Centrality of disconnected components is zero
#> ````````````````````````````````````````````````
#> Degree (normalized):
#>
#> 9715 0.14286
#> 188236 0.10204
#> 307981 0.08163
#> 71543 0.08163
#> 512309 0.08163
#>
#> Betweenness centrality (normalized):
#>
#> 9715 0.50909
#> 188236 0.47273
#> 307981 0.36364
#> 364563 0.18182
#> 73352 0.00000
#>
#> Closeness centrality (normalized):
#>
#> 305760 2.17422
#> 301645 2.13487
#> 307981 2.12892
#> 119010 1.36913
#> 71543 1.33707
#>
#> Eigenvector centrality (normalized):
#>
#> 9715 1.00000
#> 119010 0.73317
#> 71543 0.72255
#> 9753 0.67031
#> 307981 0.67026
# Calculate centralities only for the largest connected component
amgut_props3 <- netAnalyze(amgut_net1, centrLCC = TRUE,
clustMethod = "cluster_fast_greedy",
hubPar = "eigenvector")
summary(amgut_props3, showCentr = "none", clusterLCC = TRUE)
#>
#> Component sizes
#> ```````````````
#> size: 12 6 2 1
#> #: 1 1 1 30
#> ______________________________
#> Global network properties
#> `````````````````````````
#> Largest connected component (LCC):
#>
#> Relative LCC size 0.24000
#> Clustering coefficient 0.73277
#> Modularity 0.33781
#> Positive edge percentage 86.36364
#> Edge density 0.33333
#> Natural connectivity 0.19028
#> Vertex connectivity 1.00000
#> Edge connectivity 1.00000
#> Average dissimilarity* 0.82023
#> Average path length** 1.52564
#>
#> Whole network:
#>
#> Number of components 33.00000
#> Clustering coefficient 0.52341
#> Modularity 0.51212
#> Positive edge percentage 89.28571
#> Edge density 0.02286
#> Natural connectivity 0.02791
#> -----
#> *: Dissimilarity = 1 - edge weight
#> **: Path length = Units with average dissimilarity
#>
#> ______________________________
#> Clusters
#> - In the LCC
#> - Algorithm: cluster_fast_greedy
#> ````````````````````````````````
#>
#> name: 1 2 3
#> #: 4 5 3
#>
#> ______________________________
#> Hubs
#> - In alphabetical/numerical order
#> - Based on empirical quantiles of centralities
#> ```````````````````````````````````````````````
#> 119010
#> 71543
#> 9715
# Network plot
plot(amgut_props1)
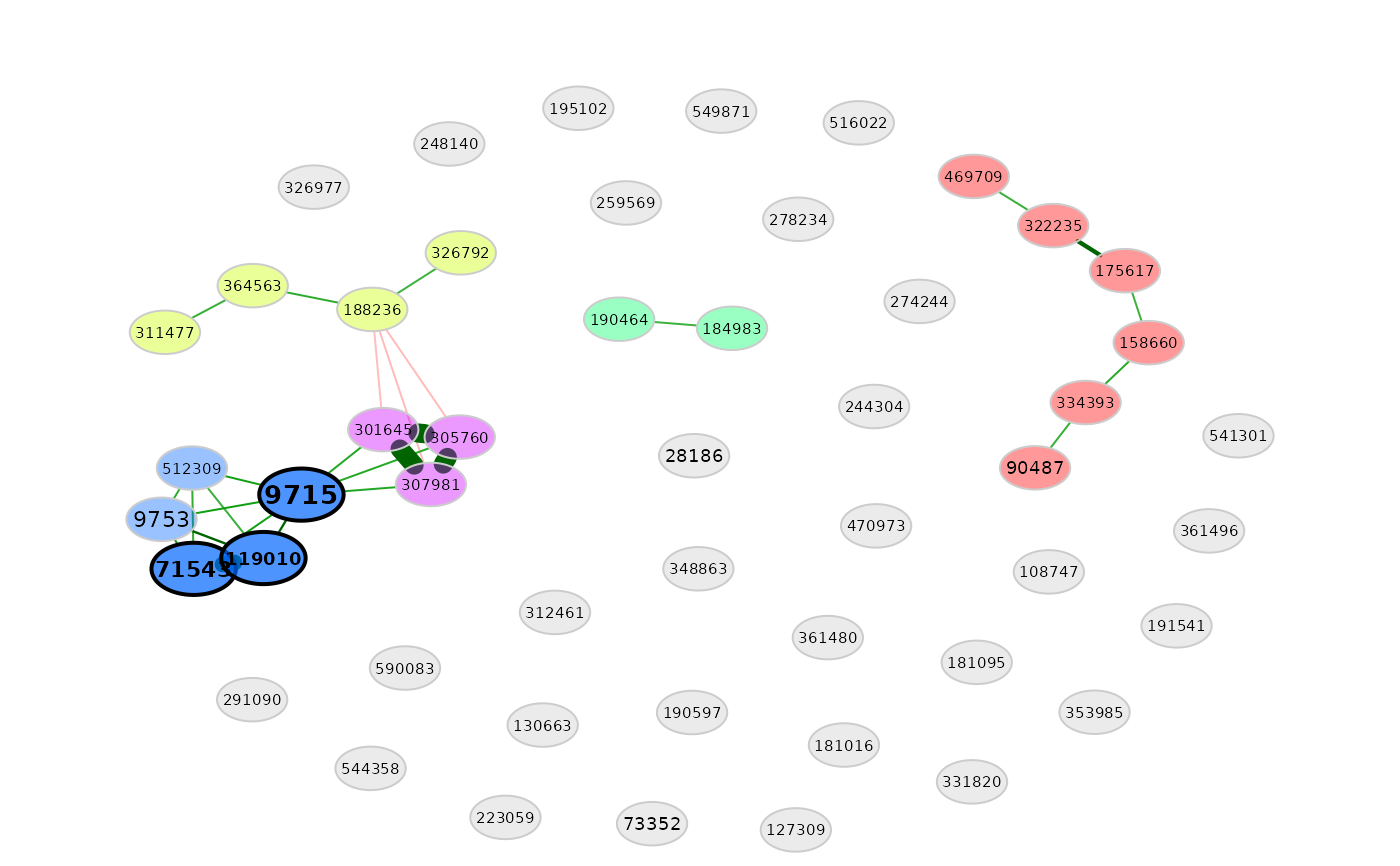 plot(amgut_props2)
plot(amgut_props2)
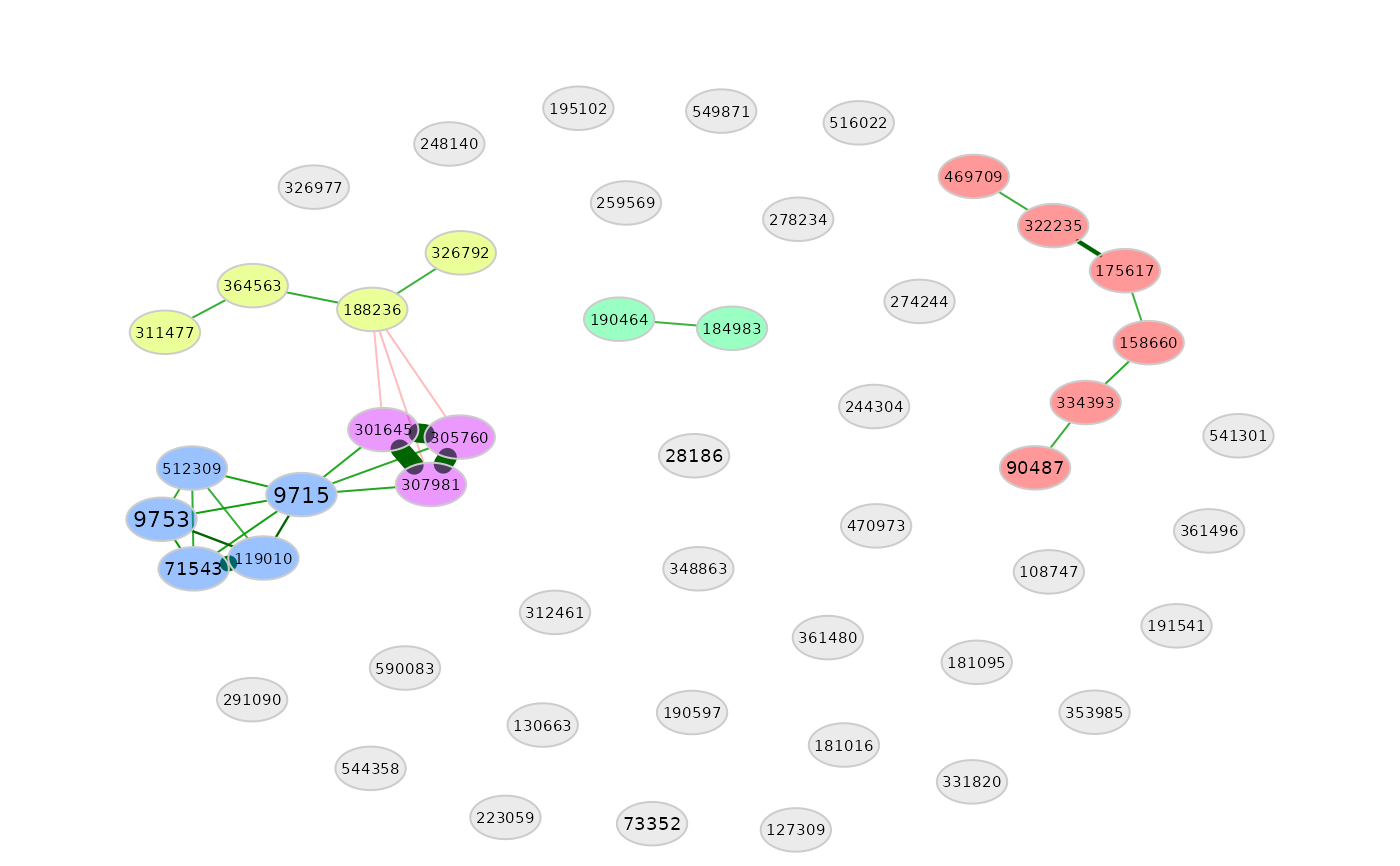 plot(amgut_props3)
plot(amgut_props3)
 #----------------------------------------------------------------------------
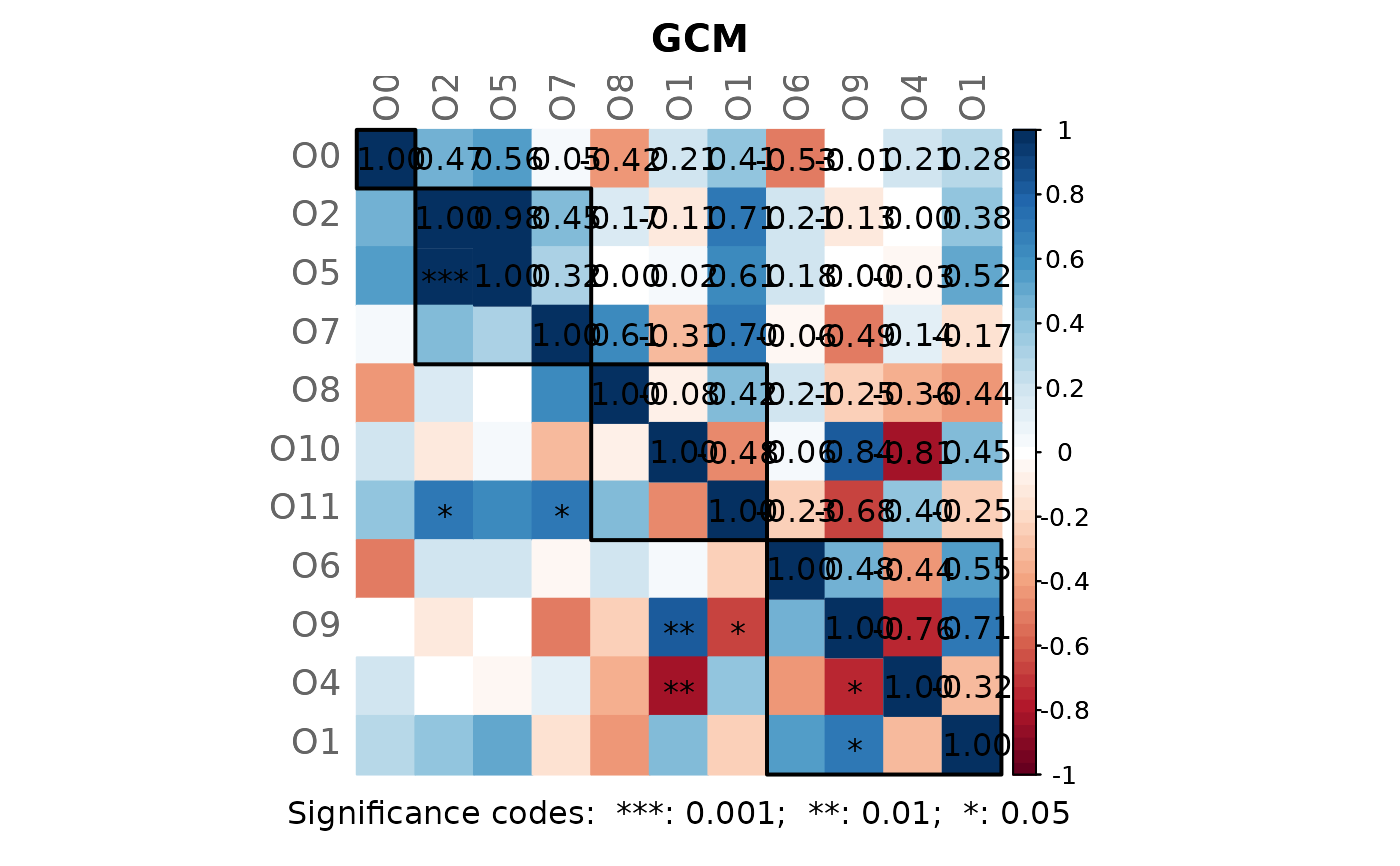
# Plot the GCM heatmap
plotHeat(mat = amgut_props1$graphletLCC$gcm1,
pmat = amgut_props1$graphletLCC$pAdjust1,
type = "mixed",
title = "GCM",
colorLim = c(-1, 1),
mar = c(2, 0, 2, 0))
# Add rectangles
graphics::rect(xleft = c( 0.5, 1.5, 4.5, 7.5),
ybottom = c(11.5, 7.5, 4.5, 0.5),
xright = c( 1.5, 4.5, 7.5, 11.5),
ytop = c(10.5, 10.5, 7.5, 4.5),
lwd = 2, xpd = NA)
text(6, -0.2, xpd = NA,
"Significance codes: ***: 0.001; **: 0.01; *: 0.05")
#----------------------------------------------------------------------------
# Plot the GCM heatmap
plotHeat(mat = amgut_props1$graphletLCC$gcm1,
pmat = amgut_props1$graphletLCC$pAdjust1,
type = "mixed",
title = "GCM",
colorLim = c(-1, 1),
mar = c(2, 0, 2, 0))
# Add rectangles
graphics::rect(xleft = c( 0.5, 1.5, 4.5, 7.5),
ybottom = c(11.5, 7.5, 4.5, 0.5),
xright = c( 1.5, 4.5, 7.5, 11.5),
ytop = c(10.5, 10.5, 7.5, 4.5),
lwd = 2, xpd = NA)
text(6, -0.2, xpd = NA,
"Significance codes: ***: 0.001; **: 0.01; *: 0.05")
 #----------------------------------------------------------------------------
# Dissimilarity-based network (where nodes are subjects)
amgut_net4 <- netConstruct(amgut1.filt, measure = "aitchison",
filtSamp = "highestFreq",
filtSampPar = list(highestFreq = 30),
zeroMethod = "multRepl", sparsMethod = "knn")
#> Checking input arguments ...
#> Done.
#> Infos about changed arguments:
#> Counts normalized to fractions for measure "aitchison".
#> Data filtering ...
#> 259 samples removed.
#> 127 taxa and 30 samples remaining.
#>
#> Zero treatment:
#> Execute multRepl() ...
#> Done.
#>
#> Normalization:
#> Counts normalized by total sum scaling.
#>
#> Calculate 'aitchison' dissimilarities ...
#> Done.
#>
#> Sparsify dissimilarities via 'knn' ...
#> Done.
amgut_props4 <- netAnalyze(amgut_net4, clustMethod = "hierarchical",
clustPar = list(k = 3))
#----------------------------------------------------------------------------
# Dissimilarity-based network (where nodes are subjects)
amgut_net4 <- netConstruct(amgut1.filt, measure = "aitchison",
filtSamp = "highestFreq",
filtSampPar = list(highestFreq = 30),
zeroMethod = "multRepl", sparsMethod = "knn")
#> Checking input arguments ...
#> Done.
#> Infos about changed arguments:
#> Counts normalized to fractions for measure "aitchison".
#> Data filtering ...
#> 259 samples removed.
#> 127 taxa and 30 samples remaining.
#>
#> Zero treatment:
#> Execute multRepl() ...
#> Done.
#>
#> Normalization:
#> Counts normalized by total sum scaling.
#>
#> Calculate 'aitchison' dissimilarities ...
#> Done.
#>
#> Sparsify dissimilarities via 'knn' ...
#> Done.
amgut_props4 <- netAnalyze(amgut_net4, clustMethod = "hierarchical",
clustPar = list(k = 3))
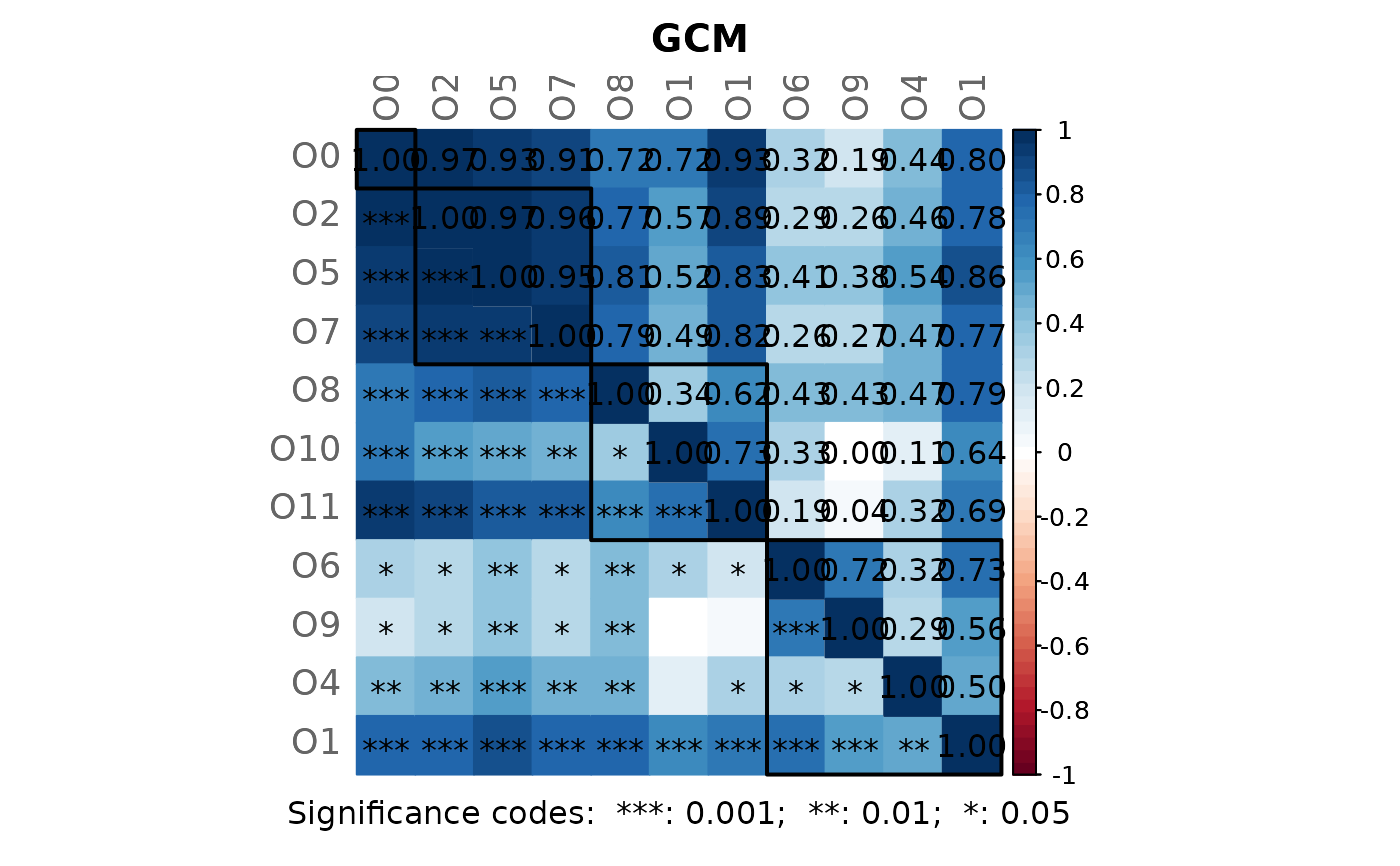 plot(amgut_props4)
plot(amgut_props4)